Introduction for the tmt package

Introduction

This package tmt provides a collection of functions to simulate data, estimate item parameters and calculation of likelihood ratio test in multistage designs (see, e.g., “Estimating item parameters in multistage designs with the tmt package in R,” n.d.; Steinfeld & Robitzsch, n.d., 2021). In multistage tests, different groups of items (module) are presented to test persons depending on their response behavior to previous item groups. Multistage testing is thus a simple form of adaptive testing. If data are collected on the basis of such a multistage design and the items are estimated using the Conditional Maximum Likelihood (CML) method, Glas (1988) has shown, that the item parameters are biased. While Eggen & Verhelst (2011) propose to avoid the bias using the marginal maximum likelihood (MML) method, Zwitser & Maris (2015) showed in their work, that taking the applied multistage design in consideration and including it in the estimation of the item parameters, the estimation of item parameters is not biased using the CML method. In this package, the approach of Zwitser & Maris (2015) is implemented. It was ensured that the necessary specification of the multistage design is as simple as possible and will be described in detail below. For the multistage design, the elementary symmetric function has to be calculated several times, so that this is as efficient as possible, the relevant functions have been written in Rcpp (Eddelbuettel & Balamuta, 2017). In addition to estimating the item parameters for multistage designs, it is also possible to estimate the item parameters for conventional designs. In order to further increase the efficiency, the algorithm of Verhelst, Glas, & Van der Sluis (1984) was used for the elementary symmetry function.

The package is well tested, but errors can still be exist. If you find a bug, please report it to us (with an working example) preferred via github: issues

Package

Below are a few sample applications of our package, which should provide information for the start:

Rasch model without multistage design

For the estimation of item parameters of a simple 1-PL model, the function tmt_rm must be called. Here only the data set has to be passed (as matrix or data.frame) to estimate item parameters. Additional arguments allow to turn off the estimates of the standard errors (for example, for time reasons) or to switch from “nlminb” to “optim” (as in the example below). Per default the items are normalized to sum = 0 as recommended by Glas (2016).

   # simulate some data 
 dat <- tmt:::sim.rm(theta = 100,b = 10,seed = c(1111,1112))
#> The specified seeds were used for the theta and beta parameters: 1111 and 1112

  # estimate item parameters
 dat.rm <- tmt_rm(dat = dat, optimization = "optim")

 # print summary
 summary(dat.rm)
#> 
#> Call:
#>   tmt_rm(dat = dat, optimization = "optim")
#> 
#> 
#> Results of Rasch model (nmst) estimation: 
#> 
#> Difficulty parameters: 
#>            est.b_i01  est.b_i02  est.b_i03 est.b_i04  est.b_i05 est.b_i06
#> Estimate   0.7735505 -0.6151232 -0.1775714 0.7193351 -1.6738525 0.7193351
#> Std. Error 0.2236931  0.2274267  0.2201498 0.2228198  0.2734564 0.2228198
#>            est.b_i07  est.b_i08  est.b_i09  est.b_i10
#> Estimate    1.343755 -0.3927773 0.03344167 -0.7300924
#> Std. Error  0.237952  0.2229743 0.21873168  0.2303699
#> 
#> CLL: -357.4132 
#> Number of iterations: 44 
#> Number of parameters: 10

Rasch model with simple multistage design

In order to estimate the item parameters in a multistage design, the corresponding design must first be specified. For the multistage design, it is necessary that each module is defined, as exemplified below with M1, M2, etc. The name of the module is arbitrary. The name of the module follows with “=~” the vector with the items of the respective path. If all modules have been defined, the start module(s) must be defined. The starting module(s) is/are described with a name and the sign “==” (double equal sign) followed by the particular module. Each path has a name followed by the “:=” character in the starting module and all other modules in that path. Each module must be followed in parentheses by the minimum (first number) and maximum (second number) of solved items in the respective module.

Keeping the syntax is very important, otherwise the design can not be translated.

component	syntax	example
module	=~	M1 =~ c(i1, i2, i3, i4, i5)
pre conditions	==	xcon(1:3)
path	:=	p1 := M2(minSolved,maxSolved)
stages	+= or ++	p1 := M2(minSolved,maxSolved) += M1(minSolved, maxSolved)

To estimate the item parameters the function tmt_rm must be called with the additional information of the multistage design. Additional arguments allow to turn off the estimates of the standard errors (for example, for time reasons) or to switch from “nlminb” to “optim” (as in the example below).

  # Example for multistage-design
  mstdesign <- "
    M1 =~ c(i1, i2, i3, i4, i5)
    M2 =~ c(i6, i7, i8, i9, i10)
    M3 =~ c(i11, i12, i13, i14, i15)

    # define path
    p1 := M2(0,2) + M1(0,5)
    p2 := M2(3,5) + M3(0,5)
  "
    # generate item parameters with corresponding names to the multistage design
  items <- seq(-1,1, length.out = 15)
  names(items) <- paste0("i",1:length(items))
  
    # generate random data under given multistage design
  dat <- tmt_sim(mstdesign = mstdesign, 
                      items = items, 
                      persons = 500)
    # estimate the item parameters under the given multistage-design
  dat.rm <- tmt_rm(dat = dat, 
                  mstdesign = mstdesign, 
                  optimization = "optim")
  
    # print summary of item parameters
  summary(dat.rm)
#> 
#> Call:
#>   tmt_rm(dat = dat, mstdesign = mstdesign, optimization = "optim")
#> 
#> 
#> Results of Rasch model (mst) estimation: 
#> 
#> Difficulty parameters: 
#>              est.b_i1   est.b_i2   est.b_i3   est.b_i4   est.b_i5   est.b_i6
#> Estimate   -0.9914007 -1.0106212 -0.7271371 -0.4511887 -0.3588835 -0.2783512
#> Std. Error  0.1514119  0.1515899  0.1497473  0.1495153  0.1497784  0.1025961
#>              est.b_i7    est.b_i8  est.b_i9 est.b_i10 est.b_i11 est.b_i12
#> Estimate   -0.4302287 -0.03525223 0.1986552 0.2552579 0.6910189 0.8959351
#> Std. Error  0.1031767  0.10227803 0.1026362 0.1028254 0.1489252 0.1499321
#>            est.b_i13 est.b_i14 est.b_i15
#> Estimate   0.6366878 0.7278017 0.8777066
#> Std. Error 0.1488105 0.1490387 0.1498052
#> 
#> CLL: -2019.943 
#> Number of iterations: 73 
#> Number of parameters: 15

Rasch model with cumulative multistage design

In order to estimate the item parameters in a cumulative multistage design, the corresponding design must first be specified. For the multistage design, it is necessary that each module is defined, as exemplified below with M1, M2, etc. The name of the module is arbitrary. The name of the module follows with “=~” the vector with the items of the respective module. If all modules have been defined, the start module(s) must be defined. The starting module(s) is/are described with a name and the sign “==” (double equal sign) followed by the particular module. Finally, all pathes must be defined. Each path has a name followed by the “:=” character in the starting module and all other modules (stages) in the path. Each module must be followed in parentheses by the minimum (first number) and maximum (second number) of solved items at that stage. For a cumulative design, the number of minimum and maximum solved items from the previous + the current module must be specified at the current stage. For this purpose the specifing character becomes “+=” instead of “+”.

Keeping the syntax is very important, otherwise the design can not be translated.

component	syntax	example
module	=~	M1 =~ c(i1, i2, i3, i4, i5)
pre conditions	==	xcon(1:3)
path	:=	p1 := M2(minSolved,maxSolved)
stages	+= or ++	p1 := M2(minSolved,maxSolved) += M1(minSolved, maxSolved)

  # Example for multistage-design
   mstdesign <- "
    M1  =~ paste0('i',21:30)
    M2  =~ paste0('i',11:20)
    M3  =~ paste0('i', 1:10)
    M4  =~ paste0('i',31:40)
    M5  =~ paste0('i',41:50)
    M6  =~ paste0('i',51:60)

    # define path
    p1 := M1(0, 5) += M2( 0,10) += M3
    p2 := M1(0, 5) += M2(11,15) += M4
    p3 := M1(6,10) += M5( 6,15) += M4
    p4 := M1(6,10) += M5(16,20) += M6
    "
    # generate item parameters with corresponding names to the multistage design
  items <- seq(-1,1, length.out = 60)
  names(items) <- paste0("i",1:length(items))
  
    # generate random data under given multistage design
  dat <- tmt_sim(mstdesign = mstdesign, 
                      items = items, 
                      persons = 1000)
    # estimate the item parameters under the given multistage-design
  dat.rm <- tmt_rm(dat = dat, 
                  mstdesign = mstdesign, 
                  optimization = "optim")
  
    # print summary of item parameters
  summary(dat.rm)
#> 
#> Call:
#>   tmt_rm(dat = dat, mstdesign = mstdesign, optimization = "optim")
#> 
#> 
#> Results of Rasch model (mst) estimation: 
#> 
#> Difficulty parameters: 
#>              est.b_i1   est.b_i2   est.b_i3   est.b_i4   est.b_i5   est.b_i6
#> Estimate   -0.8252986 -1.0050355 -0.7803577 -0.5998616 -0.6904822 -0.8477746
#> Std. Error  0.1122032  0.1123646  0.1122629  0.1129101  0.1125033  0.1121884
#>              est.b_i7   est.b_i8   est.b_i9  est.b_i10  est.b_i11  est.b_i12
#> Estimate   -0.8702415 -0.8028232 -0.6223932 -0.6451394 -0.7081800 -0.5101557
#> Std. Error  0.1121836  0.1122280  0.1127934  0.1126861  0.1004834  0.1005085
#>             est.b_i13  est.b_i14  est.b_i15  est.b_i16  est.b_i17  est.b_i18
#> Estimate   -0.5011371 -0.3836413 -0.5281863 -0.5191721 -0.3836413 -0.4108118
#> Std. Error  0.1005245  0.1008516  0.1004804  0.1004938  0.1008516  0.1007563
#>             est.b_i19  est.b_i20   est.b_i21   est.b_i22   est.b_i23
#> Estimate   -0.3472948 -0.4198583 -0.20060171 -0.24968535 -0.14686014
#> Std. Error  0.1009976  0.1007272  0.07474339  0.07490864  0.07458764
#>              est.b_i24  est.b_i25   est.b_i26   est.b_i27  est.b_i28
#> Estimate   -0.22510945 -0.1761607 -0.07874848 -0.15661458 0.11978874
#> Std. Error  0.07482314  0.0746693  0.07442789  0.07461396 0.07420146
#>              est.b_i29  est.b_i30    est.b_i31   est.b_i32  est.b_i33
#> Estimate   -0.02054247 0.02787616 -0.007713828 -0.01646654 0.11573724
#> Std. Error  0.07432460 0.07426199  0.100107300  0.10017679 0.09927797
#>             est.b_i34  est.b_i35  est.b_i36  est.b_i37  est.b_i38  est.b_i39
#> Estimate   0.17650880 0.14196262 0.19374112 0.11573724 0.27175316 0.35675700
#> Std. Error 0.09897227 0.09913779 0.09889782 0.09927797 0.09862805 0.09845915
#>             est.b_i40  est.b_i41  est.b_i42  est.b_i43  est.b_i44  est.b_i45
#> Estimate   0.54498137 0.39332583 0.33864909 0.31125080 0.32948088 0.51010966
#> Std. Error 0.09854761 0.09940186 0.09975397 0.09994955 0.09981799 0.09881883
#>             est.b_i46 est.b_i47  est.b_i48  est.b_i49  est.b_i50 est.b_i51
#> Estimate   0.51908903 0.6793613 0.64399022 0.66168523 0.64399022 0.6172340
#> Std. Error 0.09878347 0.0983786 0.09843119 0.09840228 0.09843119 0.2244367
#>            est.b_i52  est.b_i53 est.b_i54 est.b_i55 est.b_i56 est.b_i57
#> Estimate   0.3953022 0.04618896 0.7466861 0.9060721 0.5765769 0.9482369
#> Std. Error 0.2321340 0.24859002 0.2208813 0.2174207 0.2256936 0.2166721
#>            est.b_i58 est.b_i59 est.b_i60
#> Estimate   0.6598695 0.6598695 1.0281776
#> Std. Error 0.2231911 0.2231911 0.2154429
#> 
#> CLL: -15921.16 
#> Number of iterations: 162 
#> Number of parameters: 60

Likelihood-ratio Test

The likelihood ratio test of Andersen (Andersen, 1973) is also implemented. The estimated item parameters either from an simple 1-PL model or from a 1-PL model with multistage design could be passed to the function tmt_lrtest. This function is also a generic function (like tmt_rm), which calls the specific function for data with/without multistage design. For the application on very large data sets it is possible to parallelize the tmt_lrtest function. For this purpose only the amount of cores has to be passed as additional argument (it is recommended to use three cores, if possible).

    # simulate some data
  dat_nmst <- tmt:::sim.rm(theta = 100,b = 10,seed = c(1111,1112))
#> The specified seeds were used for the theta and beta parameters: 1111 and 1112

    # estimate item parameters
  dat_nmst_rm <- tmt_rm(dat = dat_nmst, optimization = "optim")
  
    # calculate likelihood ratio-test
  dat_lrt_nmst <- tmt_lrtest(dat_nmst_rm, optimization = "optim")
  
    # print summary
  summary(dat_lrt_nmst)
#> 
#> Likelihood ratio test (Andersen):
#> 
#> Value (Chi^2):  21.545
#> df (Chi^2):  9
#> p-value:  0.01

    # example of multistage-design
  mstdesign <- "
    M1 =~ c(i1, i2, i3, i4, i5)
    M2 =~ c(i6, i7, i8, i9, i10)
    M3 =~ c(i11, i12, i13, i14, i15)

    # define path
    p1 := M2(0,2) + M1(0,5)
    p2 := M2(3,5) + M3(0,5)
  "
    # generate item parameters with corresponding names to the multistage design
  items <- seq(-1,1, length.out = 15)
  names(items) <- paste0("i",1:length(items))
  
      # generate random data under given multistage design
    dat_mst <- tmt_sim(mstdesign = mstdesign, 
                      items = items, 
                      persons = 500,
                      seed = 1111)

    # estimate the item parameters under the given multistage-design
  dat_mst_rm <- tmt_rm(dat = dat_mst, 
                  mstdesign = mstdesign, 
                  optimization = "optim")

    # calculate likelihood ratio-test
  dat_lrt_mst <- tmt_lrtest(dat_mst_rm, optimization = "optim")
  
    # print summary
  summary(dat_lrt_mst)
#> 
#> Likelihood ratio test (Andersen) for multistage designs:
#> 
#> Value (Chi^2):  8.44
#> df (Chi^2):  14
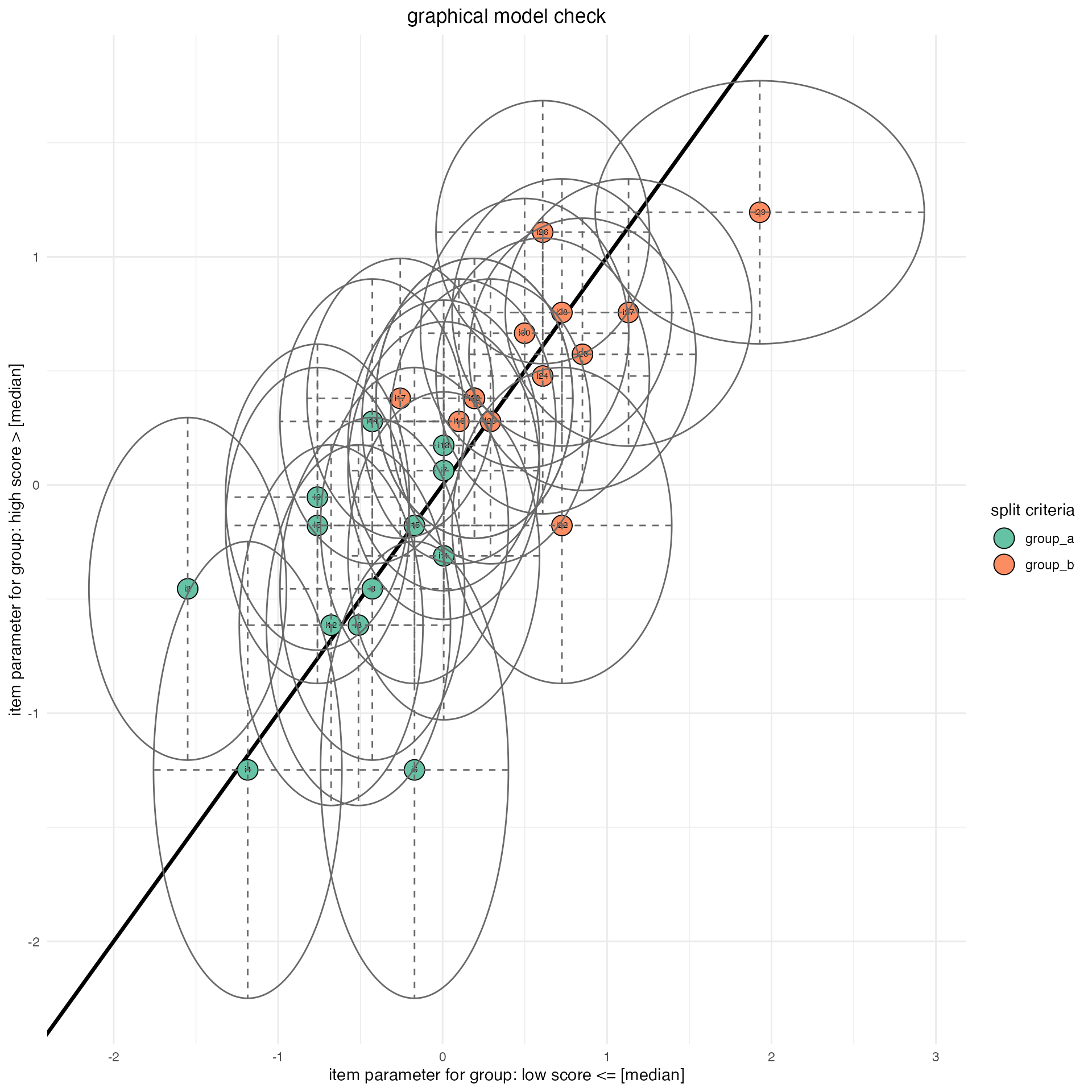
#> p-value:  0.865

Graphical model check

For a graphical comparison of estimated item parameters for each sub group, we provide a so-called graphical model check. Several options are available for further specification of the plot (internally the package ggplot2 is used)

    # example of multistage-design
  items <- seq(-1,1,length.out = 30)
  names(items) <- paste0("i",1:30)
  persons = 100
  mean = 0
  sd = 1
  dat <- tmt:::sim.rm(theta = persons, b = items, c(1111,1112))
  
  dat.rm <- tmt_rm(dat, optimization = "optim")
  dat.lrt <- tmt_lrtest(dat.rm, split = "median", optimization = "optim")


  info <- rep(c("group_a","group_b"),each = 15)
  names(info) <- paste0("i",1:30)

  drop <- c("i1","i18","i20","i10")

  tmt_gmc(object = dat.lrt, 
    ellipse = TRUE, 
    info = info,
    drop = drop,
    title = "graphical model check",
    alpha = 0.05,
    legendtitle = "split criteria")

References

Andersen, E. B. (1973). A goodness of fit test for the Rasch model. Psychometrika, 38(1), 123–140. doi:10.1007/BF02291180

Eddelbuettel, D., & Balamuta, J. J. (2017). Extending extitR with extitC++: A Brief Introduction to extitRcpp. PeerJ Preprints, 5, e3188v1. doi:10.7287/peerj.preprints.3188v1

Eggen, T. J. H. M., & Verhelst, N. D. (2011). Item Calibration in Incomplete Testing Designs. Psicologica: International Journal of Methodology and Experimental Psychology, 32(1), 107–132.

Estimating item parameters in multistage designs with the tmt package in R. (n.d.).

Glas, C. A. W. (1988). The Rasch model and multistage testing. Journal of Educational Statistics, 13(1), 45–52. doi:10.3102/10769986013001045

Glas, C. A. W. (2016). Maximum-likelihood estimation. In W. J. van der Linden (Ed.), Handbook of item response theory: Volume two: Statistical tools (pp. 197–236). New York, NY: CRC Pres. doi:10.1007/978-1-4612-4230-7_5

Steinfeld, J., & Robitzsch, A. (n.d.). Conditional maximum likelihood estimation in probability-based multistage designs. Behaviormetrika, x(x), xxx–xxx.

Steinfeld, J., & Robitzsch, A. (2021). Item parameter estimation in multistage designs: A comparison of different estimation approaches for the Rasch model. Psych, 3(3), 279–307. doi:10.3390/psych3030022

Verhelst, N., Glas, C. A. W., & Van der Sluis, A. (1984). Estimation problems in the rasch model: The basic symmetric functions. Computational Statistics Quarterly, 1(3), 245–262. doi:10.1177/014662169602000206

Zwitser, R. J., & Maris, G. (2015). Conditional statistical inference with multistage testing designs. Psychometrika, 80(1), 65–84. doi:10.1007/s11336-013-9369-6

Jan Steinfeld & Alexander Robitzsch

May 03, 2024